Implementations, Simulations, and Abstraction Functions
Programmers often talk about implementing data abstractions, algorithms, or specifications. All three of these cases have something interesting in common. On the one hand, they each involve an abstract entity that is defined by a set of expected behaviors. On the other, there are many different possible realizations of the abstract entity in question.
In this post, we’re going to explore some methods in computer science for characterizing this relation between abstract entities and their possible implementations. We’re going to treat our abstract entities as abstract state machines. And we’re going to view implementations as simulations of the relevant abstract state machine. Finally, we’re going to explore a method for checking whether a supposed implementation is successful, using what are called abstraction functions.
State Machines
A state machine is composed of:
- [ST1] A set $S$ of possible states ${s_1, s_2, …}$.
- [ST2] A set $I \subseteq S$ of initial states ${i_1, i_2, …}$.
- [ST3] A set of actions $A = {a_1, a_2, …}$.
- [ST4] A set of transitions of the form $(s_i, a_j, s_k)$.
Here’s a simple example, with states ${s_1, s_2, s_3}$, initial state $i_1 = s_1$, actions ${a, b, c}$, and transitions $(s_1, a, s_2)$, $(s_1, b, s_3)$, $(s_2, c, s_3)$, and $(s_3, a, s_1)$.
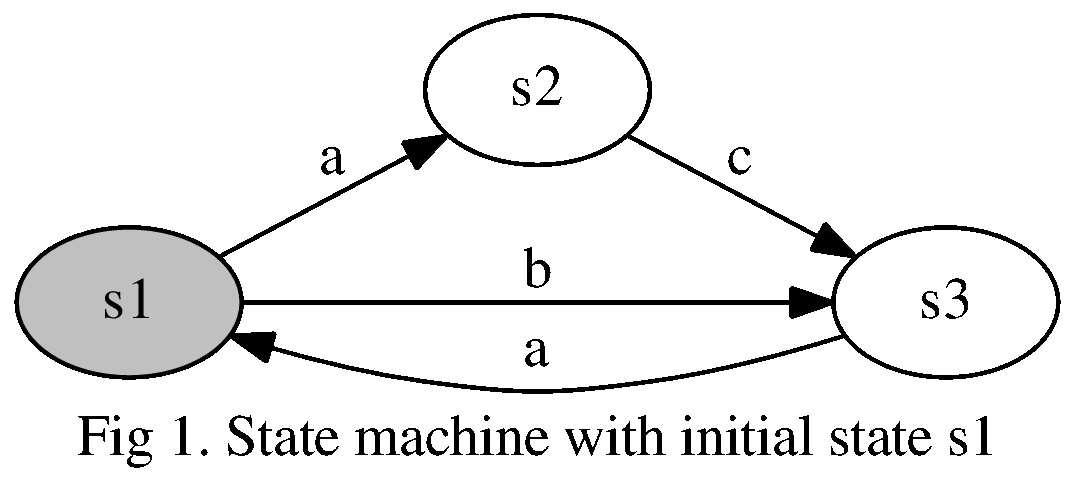
Our machine begins in state $s_1$ (highlighted to indicate it’s an initial state). If our machine is in state $s_1$, then action $a$ will transition it to state $s_2$. From there action $c$ will transition to $s_3$, etc. The state machine can only be in one state at a time. And notice that the same action can show up in different transitions. Here we see that from $s_1$, $a$ transitions the machine to $s_2$, but from $s_3$, $a$ transitions the machine to $s_1$.
We can view a data structure, algorithm, or specification as an abstract state machine. As an example, consider a stack:
- [ST1] $S_{st}$ is the set of all ordered $n$-tuples including the empty tuple.
- [ST2] For simplicity, we can say that $I$ has one member: the empty tuple. This captures the idea that a stack starts out empty.
- [ST3] $A = {push(), pop(), peek()}$.
To be precise, we’d have to allow for a separate $push()$ action for every possible item that could be pushed onto the stack. Here’s a subgraph of our stack state machine representing a small subset of states and transitions:
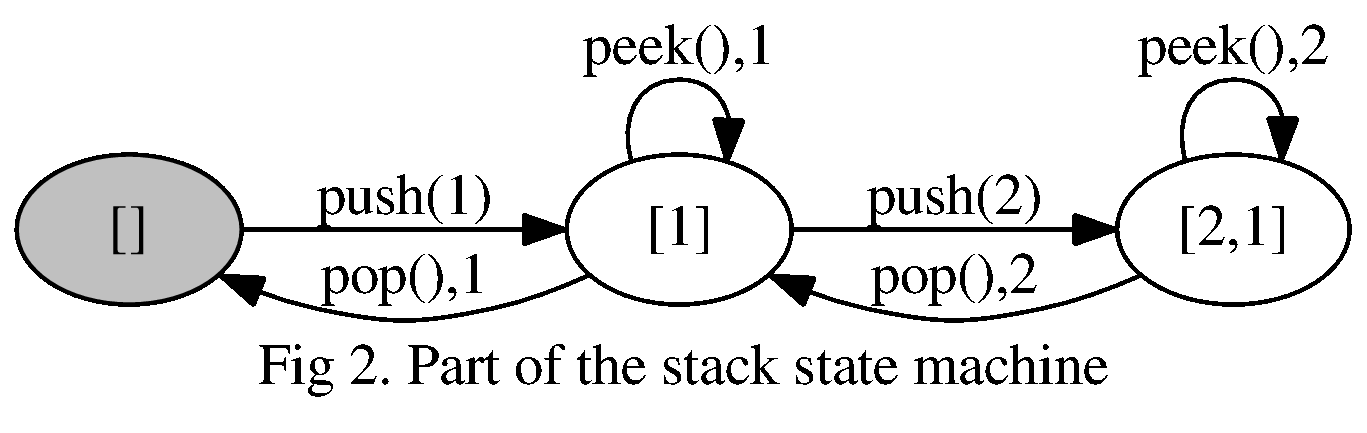
$peek()$ is a transition function from a state to itself, returning the top of the stack to the client. $push()$ and $pop()$ change the state of the stack, as represented by the transitions in the diagram. $pop()$ also returns the top of the stack to the client. These are exactly the behaviors we would expect of a stack.
Distributed systems provide another kind of example. One way to think of a certain type of distributed system is as a simulation of a single machine by a network of separate machines. We can use an abstract state machine to model a single machine and then investigate our distributed implementation in terms of that.
Let’s say we’re interested in building a distributed key/value store. If we were dealing with a run of the mill key/value store on a single machine, we should expect the following to be respected:
- [KV1] At any time $t$, a key $k_i$ is present or not.
- [KV2] At any time $t$, there is a unique value $v_i$ for each present key $k_i$.
- [KV3] Updates happen in a determinate order.
- [KV4] A read of $k_i$ provides the latest value for $k_i$.
These conditions are embedded in the following state machine:
- [ST1] $S_{kv}$ is the set of all configurations of keys and values, where a configuration is a subset of ${k_1, k_2, …}$ paired with corresponding values. For example, ${(k_1, 4), (k_4, 10)}$ or ${(k_2, 20), (k_3, 9), (k_{10}, 3)}$ are two possible configurations. When constructing a configuration, we begin with a subset of ${k_1, k_2, …}$, thereby assuring that each $k_i$ is only represented at most once.
- [ST2] For simplicity, we can say that $I$ has only one member: the empty configuration ${}$. This captures the idea that a key/value store starts out empty.
- [ST3] $A = {get(), put(), delete()}$. Technically, we have to allow a separate $get()$ and $delete()$ action for each key $k_i$ and a separate $put()$ action for each key/value pair $(k_i, v_j)$.
Here’s a subgraph of our key/value state machine representing a small subset of possible key/value pairs and actions:
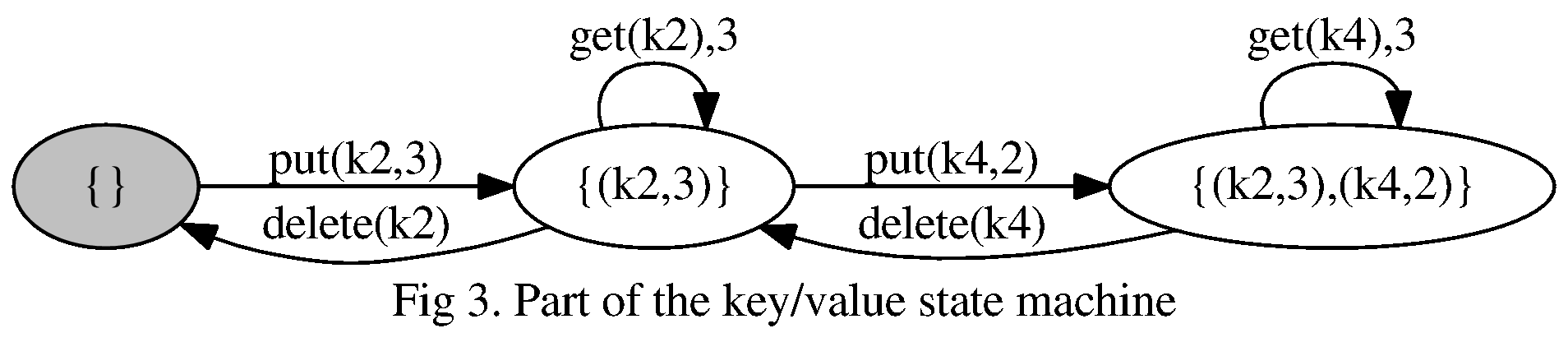
This state machine gives us KV1 and KV2 by the definition of $S_{kv}$. Each key $k_i$ is present at most once and, if present, has exactly one value.
KV3 is guaranteed by the fact that a deterministic state machine always transitions in a determinate order, so we can always point to a temporally ordered history of state transitions.
KV4 is guaranteed by KV3 combined with (a) the fact that a state machine is always in one state and (b) the definition of our state space as the set of configurations, where a configuration is composed of pairs of all present (unique) keys and their corresponding values.
A distributed key/value store with replicated data, on the other hand, does not “really” meet the conditions KV1-KV4 described above. Consider the state space for such a system. We have more to consider than a single configuration per state. Instead, we must assign a configuration to each of $N$ nodes in the network. So a state for a network with two nodes $n_1$ and $n_2$ might look like
$n_1: {(k_1, 4)},$ $n_2: {(k_1, 3), (k_2, 10)}$
With these more complex states in mind, let’s consider each of KV1-KV4 for our distributed system:
- [KV1'] $k_i$ may be present on node $n_1$ but not $n_2$ (for example, if a replication message has not yet reached $n_2$).
- [KV2'] While $k_i$ has value $v_i$ on $n_1$, it might have value $v_j$ on $n_2$ (for example, if an update has not yet propagated to $n_2$).
- [KV3'] Different nodes might receive updates in some order that cannot be globally determined because of a lack of a global clock.
- [KV4'] Consider the situation in KV2'. A read of $k_i$ might provide the latest value if executed on $n_1$, which already has $v_i$, but not if executed on $n_2$, which still has $v_j$.
The distributed key/value store technically fails to meet all four of our conditions. But what’s most important is that it appears like a single system to the client. If we can design our system in such a way that a client could never distinguish its behavior from that of a single system, then we probably have all that we need.
Traces
We can make this intuition more precise. Call anything that a client can see an external behavior of the system. In a real world single-system key/value store, the client calls $get(k_2)$ and receives a value in return. It’s unaware of whatever steps the system took to look up the key, retrieve the value, and (possibly) transform it into a form the client recognizes. Furthermore, it’s unaware of any transitory states the system might have entered to carry out these steps. These are all internal behaviors of the system.
From the client’s point of view, only the external behavior matters. It is only on the basis of external behavior that it can distinguish one state of the system from another. So when we say we’d like to design a distributed system in such a way that a client can never distinguish its behavior from that of a single system, we should focus on the external behavior.
The history of external behaviors of a system is called a trace. The set of all possible traces defines that system from the client’s point of view. Let’s distinguish a trace of a system from an execution. By execution, we mean to include internal as well as external behaviors. The crucial point to keep in mind is that a single trace can be realized by many different executions.
Consider a contrived example: we have two implementations of a stack. They both use a linked list (cleverly called $list$) to represent their data. The first one implements the stack API in a familiar way:
$Stack_1$ $push(a) := { list = a::list; }$ $peek() := { return$ $list.head; }$ $pop() := { list = list.tail; return$ $list.head; }$
Our second implementation relies on a more convoluted scheme. It keeps $list$ in reverse order for some inexplicable reason. It then implements the stack API as follows:
$Stack_2$ $push(a) := { list = (a::(list.reverse)).reverse; }$ $peek() := { return$ $(list.reverse).head; }$ $pop() := { h = (list.reverse).head; list = ((list.reverse).tail).reverse; return$ $h; }$
Despite the weird internal steps $Stack_2$ takes involving reverse, its traces are indistinguishable from those of $Stack_1$. As far as the client is concerned, these two versions of a stack are the same (excluding performance considerations). For any series of API calls by the client, we would have two different executions but the same trace. Furthermore, from the client’s perspective, we can describe these traces by the same state machine diagram. Intuitively, they both implement the same abstract state machine.
Let’s make this intuition more precise by considering what it means for one system to $simulate$ another.
Simulations
Say we have some system $X$ that is designed to simulate a target system $T$. What must be true in order for $X$ to count as a successful simulation?
For one thing, $X$ must never do anything that $T$ couldn’t do. A simulation should be limited to the behaviors of its target. We can express this idea in terms of traces.
We’ll use $X^{trace}$ to denote the set of all possible traces of $X$. From the client’s point of view, $X^{trace}$ defines $X$, since it encompasses all the possible sequences of external behaviors of $X$.
If $X$ successfully simulates $T$, then it should be limited to possible traces of $T$. Formally, we can express this condition as
- [SIM1] $X^{trace} \subseteq T^{trace}$.
SIM1 says that if $X$ simulates $T$, then any trace of $X$ is a trace of $T$.
We can also express our intuition in terms of safety and liveness, two concepts taken from the distributed systems literature. A safety property of a set of traces is a property that holds for any step in any trace in the set. Safety properties say that something bad will never happen. KV1-KV4 above are examples of safety properties for a single system key/value store.
Take KV2, the requirement that any given key has at most one value at any one time. This property ensures that at any step in any trace of our key/value store, we are guaranteed to have at most one value for any given key.
A liveness property for a set of traces guarantees that any trace in the set contains a step in which that property holds. Liveness properties say that something good will happen. For example, if we say a system must eventually terminate, then we are talking about a liveness property of the system. For $X^{trace}$, this would mean that every trace in $X^{trace}$ contains a termination step.
We can use these concepts to further refine our model of simulations. Again, consider a simulation $X$ of some target $T$. If a safety property holds for $T$, then it must also hold for $X$. Think of it this way. If a client is guaranteed that $T$ will never do something bad, then a successful simulation $X$ must respect that guarantee.
On the other hand, if a liveness property holds for $T$, it is not necessarily true that it holds for $X$. Why is that? It’s because traces can be infinite in length. Imagine that a client is guaranteed that $T$ will eventually do something good. If $X$ lacks this liveness property but every trace of $X$ is infinite in length, the client will never be able to determine that $X$ lacks the property. This is because the client could always wonder whether any given infinite trace of $X$ might exhibit the property at some later time.
However, if a liveness property holds for $X$, then it must hold for $T$. This is because we can be certain that every trace of $X$ will eventually exhibit the guaranteed property. However, if a trace of $X$ contains some step $x_i$ for which the property holds, then so must some trace of $T$. This follows from SIM1 above.
Using the notation $s(X)$ and $l(X)$ for ascribing the safety and liveness properties to $X$, we can now add the following conditions for successful simulation:
- [SIM2] If $s(T)$, then $s(X)$
- [SIM3] If $l(X)$, then $l(T)$
You may have noticed that SIM1 entails SIM2 and SIM3. But it can be useful to separate these concepts out to get a clearer sense of how $X^{trace}$ and $T^{trace}$ are related.
We have left out one important, and perhaps obvious, point. If a client is the one issuing commands to $X$, then it must be the case that $X$ is able to process the same set of commands as $T$. This ensures that $X^{trace}$ cannot be arbitrarily small. Though it can be a proper subset of $T^{trace}$, it must still capture all the traces the client would expect to encounter through any series of issued commands.
We have now made precise our earlier intuition that a successful simulation should be indistinguishable from its target to a client. If $X$ successfully simulates $T$, then a client will never be able to tell that $X$ and $T$ are distinct.
In thinking about simulations, we have focused entirely on external behaviors, the kind of thing a client can see. But different successful implementations can exhibit divergent internal behaviors, as we saw with our stack implementations above. So we still have to account for the relationship between the idiosyncratic states and transitions of a given implementation, on the one hand, and the states and transitions of the abstract state machine it is implementing, on the other. For that reason, we now turn to abstraction functions.
Abstraction Functions
We have seen that many internal executions can correspond to one external trace. This is directly related to our central question: what is the relationship between an abstract state machine and its implementations? When we move from the idiosyncratic states and transitions of an implementation to the shared target states and transitions of the corresponding abstract state machine, we are moving up the “abstraction ladder”. For example, we say that $Stack_1$ and $Stack_2$ are both examples of a stack. Here the concept of a stack is more abstract than $Stack_1$ or $Stack_2$. These are familiar ideas, but how do we make them precise?
What we need is a way to map states of an implementation to the corresponding states of the target abstract state machine. With such a method, we can describe the states of the implementation in the more abstract language of the specification. To anticipate, we will find that there is a many-to-one relation between the states of the implementation and the states of the target abstract state machine. The implementation encapsulates details (states and transitions) that can be safely ignored by a client. The client need only think in terms of the abstract state machine.
What we need is an abstraction function, which we will call $f$. $f$ is a total function from the states of our implementation $X$ into the states of our target $T$. This means that $f$ maps each state of $X$ to a state of $T$.
Returning to our stack example, $Stack_2$ moves through a number of states related to reversing its internal $list$ whenever it is updated. However, none of these internal states are accessible to the client. What this means is that once $Stack_2$ has received a command, say $pop()$, it seems to the client as though it immediately transitions to the next corresponding state in the abstract state machine. This is because all the client can do to interact with it is to issue another command. But $Stack_2$ will only execute this next command once it has finished processing $pop()$. So we can safely map all the intermediate internal steps of $Stack_2$ to a single state of the abstract state machine for stack.
Given an abstraction function $f: X \to T$, how do we prove that $X$ successfully implements $T$? We could do this through induction. As with any inductive argument, we would need to establish our base and our inductive step. Taking $tr(s, s')$ to denote the existence of a transition from $s$ to $s'$, we need to show the following:
- [Base] If $s_i$ is an initial state of $X$, then $f(s_i)$ is an initial state of $T$.
- [Inductive Step] If $tr(s, s')$, then $tr(f(s), f(s'))$, assuming the identity transition exists for every state in $T$.
Base says that every initial state of $X$ corresponds to an initial state of $T$. Inductive Step says that any transition internal to $X$ corresponds to a transition in $T$. We must assume the existence of the identity transition (that is, the transition from a state to itself) in $T$ because transitions internal to $X$ might all be subsumed under one state in $T$, as we were just discussing in relation to $Stack_2$.
If we can establish both Base and Inductive Step, then by induction we’ve shown that every execution of $X$ corresponds to a trace of $T$. And this also means we’ve shown that $X$ simulates $T$. That’s because we’ve shown that the set of traces of $X$ is a subset of the set of traces of $T$, thereby satisfying SIM1 (and hence SIM2 and SIM3). So the induction above provides a template for constructing a proof that some $X$ implements some target $T$.
As a final example, recall our distributed key/value store from earlier. We noticed that, strictly speaking, it failed to meet any of conditions KV1-KV4. That was because of the possibility of inconsistencies between nodes at any particular point in time. However, if we can find an abstraction function that maps states of the distributed system to states of a single system key/value store, then we can show that it actually does satisfy KV1-KV4 from the client’s point of view. Much of the work on distributed systems amounts to designing systems for which such an abstraction function could be defined.
Conclusion
We’ve explored some methods in computer science for characterizing the implements relation. We’ve viewed implementation targets (whether data abstractions, specifications, or single systems) as abstract state machines. And we’ve interpreted implementations as simulations of those abstract state machines. We’ve looked at some criteria for successful simulations and considered how abstraction functions can help us think about the relationship between the internal states of an implementation and the states of the abstract state machine it’s simulating.
These conceptual tools may not be of any particular use in designing implementations, but they can help us think about what it means to be a successful implementation, and how we might go about proving that a particular implementation is successful.
References
[1] B. Alpern and F. Schneider. Defining liveness. Information Processing Letters 21,4, 1985.
[2] L. Lamport. A simple approach to specifying concurrent systems. Comm. ACM, 32,1, Jan. 1989.
[3] B. W. Lampson. How to build a highly available system using consensus. Lecture Notes in Computer Science, Vol. 1151, 1996.
[4] R. Milner. Communicating and Mobile Systems: the Pi-Calculus. Cambridge University Press, 1999.